Puppet model

Puppet model is a contour body model parametrized by pose and shape, as illustrated on the right side. It is a part-based model, where each part is represented by a closed contour. The contour points of body parts are generated in local coordinate systems by linear models in the form

where $\textbf{p}_i$ are contour points, $\textbf{y}_i$ are joint points for the $\textit{i}$-th body part, $\textbf{B}_i$ is the matrix of PCA (Principal Component Analysis) components, $\textbf{z}_i$ are PCA coefficients, and $\textbf{m}_i$ is the part mean.

The PCA bases $\textbf{B}_i$ are learned from 2D projections of a realistic, 3D human body model.The coefficients $\textbf{z}_i$ here are pose-dependent shape deformations. They do not model variability of intrinsic body shape (tall, short, fat, slim) as the model is learned from a single 3D body model.

Each puppet contains 10 body parts connected by 13 joints (shoulder, elbow, wrist, hip, knee, ankle, neck) and two landmarks (face and belly). We construct puppets in 16 viewpoints across the 360 degree radial space in the transverse plane.

More details on the puppet model can be found in ( Zuffi et al, 2012).

Annotaing with a puppet model

The annotation involves adjusting the joint position so that the contours of the puppet align with image information. In contrast to simple joint or limb annotations, the puppet model guarantees realistic limb size proportions, in particular in the context of occlusions, and also provides an approximate 2D shape of the human body. The annotation is done using Amazon Mechanical Turk. To aid annotators, we provide the posed puppet on the first frame of each video clip. For each subsequent frame the interface initializes the joint positions and the scale with those of the previous frame. We manually correct annotation errors during a post-annotation screening process.

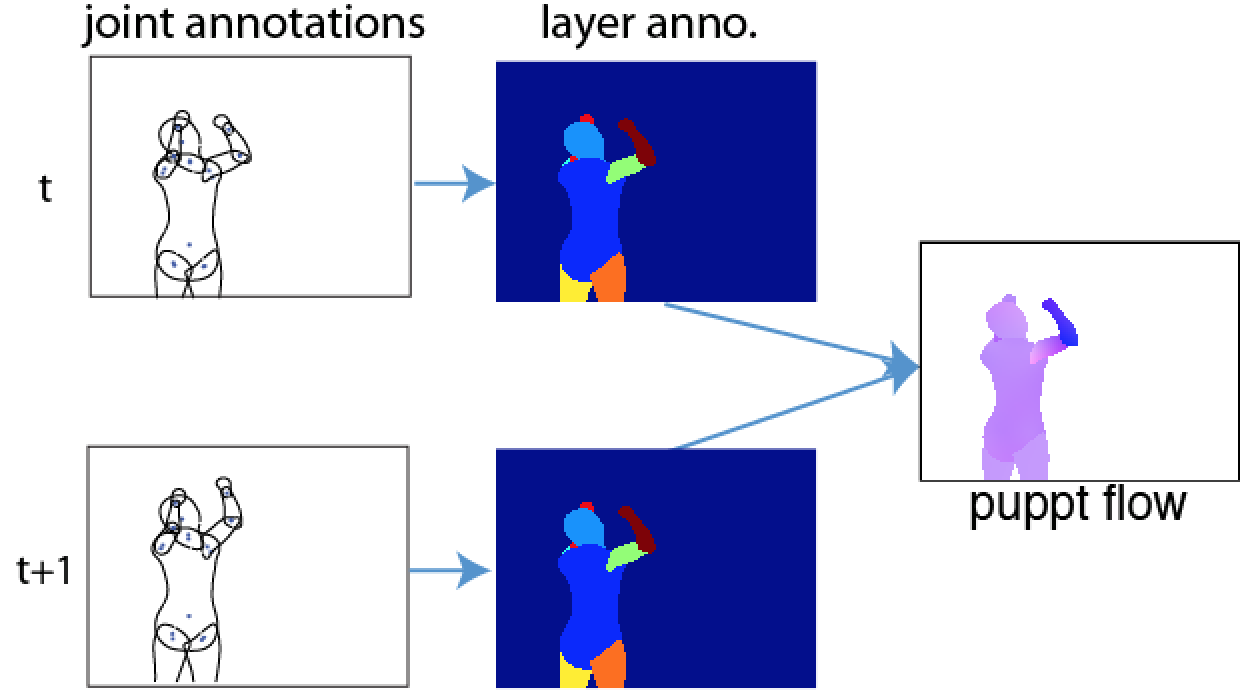
Puppet flow

Puppet Flow is based on the puppet model representation of the human body. Given two instances of the puppet model in adjacent frames, we define a per-pixel motion vector by the warping transformation that maps the points of the first puppet into the second puppet. This warping function is estimated from contour points of each body part. For a puppet model of $N$ parts,the puppet flow is defined as:

$\sum_{i=1}^N D(\textbf{p}_{t,i}) \circ W^{i}_{t,t+1}(\textbf{p}_{t,i},\textbf{p}_{t+1,i})$

where $D(\textbf{p}_{t,i})$ is the mask for the $\textit{i}$-th body part at time $t$, $\textbf{p}_{t,i}$ are the points that belong to the $\textit{i}$-th body part at time $t$, $W^{i}_{t,t+1}(\textbf{p}_{t,i}, \textbf{p}_{t+1,i})$ is a part-specific warping function. It is estimated by the deformation of contour points of the part $\textit{i}$ at time $t$ $(\textbf{p}_{t,i})$ into the corresponding points at time $t+1$ $(\textbf{p}_{t+1,i})$. Here we use Thin Plate Splines (TPS) as the warping function ( Bookstein, 1989).

Also see the technical report for details ( Zuffi and Black, 2013).

As an example, Fig. 1 shown below shows a puppet and the mask for 10 body parts $(D(\textbf{p}_{t,i}))$ at time $t$, Fig. 2 shows the puppet at time $t+1$. The left lower arm of the puppet moves downward by 100 pixels while the rest of body parts stay still. Fig. 3 shows the pupppet flow. It is zero in all the body parts except for the left lower arm.

Reference

(Zuffi et al, 2012) S. Zuffi, O. Freifeld, and M. J. Black. From pictorial structures to deformable structures. In CVPR, pages 3546–3553, 2012.

(Bookstein, 1989) F. L. Bookstein. Principal warps: Thin-plate splines and the decomposition of deformations. IEEE Trans. Pattern Anal. Mach. Intell., 11(6):567–585, 1989.

(Zuffi and Black, 2013) S. Zuffi and M. J. Black. Puppet flow. Technical Report TRIS-MPI-007, MPI for Intelligent Systems, 2013.